不用去学校,就能修名校专科/本科学历,国家承认 学信网可查,查看详情>>>
学习推荐本试卷总分100分,测试时间150分钟。
一、单项选择题(每小题2分,共10分)
2.设y=cos![]() ,则( )
,则( )
A.当x→0时,y为无穷小量
B.当x→0时y为无穷大量
C.在区间(0,1)内y为无界变量
D.在区间(0,1)内y为有界变量
3.级数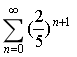 的和s=( )
的和s=( )
A.3/2
B.5/3
C.2/5
D.2/3
5.矩阵A=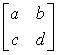 为非奇异矩阵的充要条件是( )
为非奇异矩阵的充要条件是( )
A.ad-bc≠0
B.ad-bc=0
C.ab-cd=0
D.ab-cd≠0
1.函数y=loga(x^2-4)(a是常数且a>0,a≠1)的定义域是( )
A.(2,+∞)
B.(-∞,-2)∪(2,+∞)
C.(-∞,-2]∪[2,+∞)
D.(-∞,-2)
4.![]() ( ).
( ).
A.
B.
C.
D.
二、填空题(每小题3分,共30分)
1.设f (x)=x^2,g(x)=e^x,则f [g(x)]=_________.
5.函数y=(x-2)^2在区间[0,4]上的最小值是_________.
7.行列式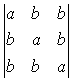 =_________.
=_________.
8.设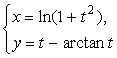 ,则
,则![]() =_________.
=_________.
10.设矩阵A=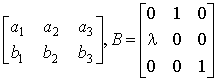 ,则AB=_________.
,则AB=_________.
4.d(sin2x+cosx)=_________dx.
6.若F(x)与G(x)均为f (x)在区间I上的原函数,则F(x)与G(x)相差一个_________.
2.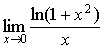 =_________.
=_________.
9.若无穷限反常积分![]() ,则常数k=_________.
,则常数k=_________.
3.设f (x)=e^(5x),则f′(0)=_________.
三、计算题(每小题6分,共48分)
1.求极限![]() .
.
3.求微分方程e^(x-y)dx-dy=0的通解.
2.求不定积分![]() .
.
5.计算定积分![]() .
.
4.求曲线y=![]() 在点(1/2,2)处的切线方程.
在点(1/2,2)处的切线方程.
6.判定函数f (x)=arctanx-x的单调性.
8.当λ取什么值时齐次性线方程组 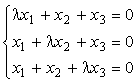 只有零解.
只有零解.
7.设y=![]() ,求y′.
,求y′.
四、综合题(每小题6分,共12分)
2.求由直线y=x与抛物线y^2=x所围成的平面图形的面积.
1.求函数y=x-ln(1+x)的极值.
转载请注明:文章转载自(http://www.gdzkw.net)